背景:
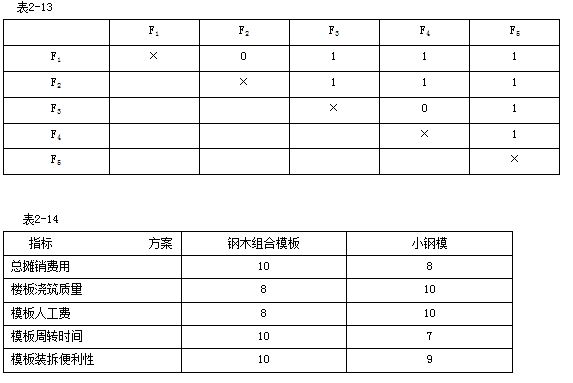
承包商B在某高层住宅楼的现浇楼板施工中,拟采用钢木组合模板体系或小钢模体系施工。经有关专家讨论,决定从模板总摊销费用(F1)、楼板浇筑质量(F2)、模板人工费(F3)、模板周转时间(F4)、模板装拆便利性(F5)等五个技术经济指标对该两个方案进行评价,并采用0-1评分法对各技术经济指标的重要程度进行评分,其部分结果见表2-13,两方案各技术经济指标的得分见表2-14。
经造价工程师估算,钢木组合模板在该工程的总摊销费用为40万元,每平方米楼板的模板人工费为8.5元;小钢模在该工程的总摊销费用为50万元,每平方米楼板的模板人工费为6.8元。该住宅楼的楼板工程量为2.5万m2。
问题:
1. 试确定各技术经济指标的权重(计算结果保留三位小数)。
2. 若以楼板工程的单方模板费用作为成本比较对象,试用价值指数法选择较经济的模
板体系(功能指数、成本指数、价值指数的计算结果均保留二位小数)。
3. 若该承包商准备参加另一幢高层办公楼的投标,为提高竞争能力,公司决定模板总
摊销费用仍按本住宅楼考虑,其他有关条件均不变。该办公楼的现浇楼板工程量至少要达到多少平方米才应采用小钢模体系(计算结果保留二位小数)?
答案:
问题1:
解:根据0-1评分法的计分办法将表2-13中的空缺部分补齐后再计算各技术经济指标的得分,进而确定其权重。
0-1评分法的特点是:两指标(或功能)相比较时,不论两者的重要程度相差多大,较重要的得1分,较不重要的得0分。在运用0-1评分法时还需注意,采用0-1评分法确定指标重要程度得分时,会出现合计得分为零的指标(或功能),需要将各指标合计得分分别加1进行修正后再计算其权重。根据0-1评分法的计分办法,两指标(或功能)相比较时,较重要的指标得1分,另一较不重要的指标得0分。
各技术经济指标得分和权重的计算结果见表2-15。
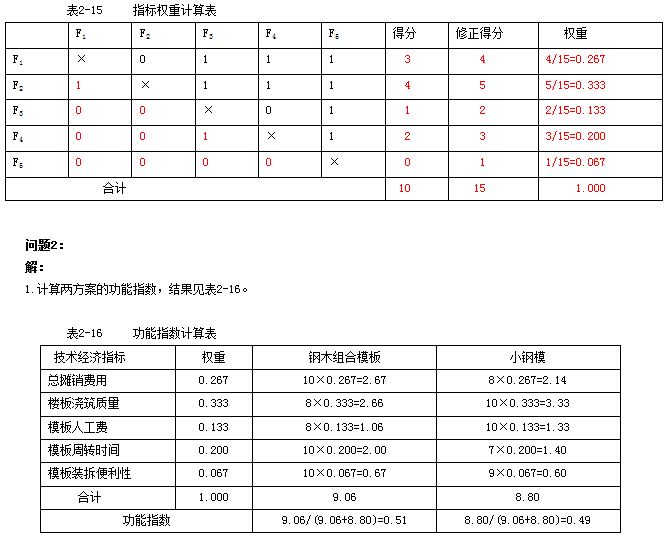
2.计算两方案的成本指数
钢木组合模板的单方模板费用为: 40/2.5+8.5=24.5(元/m2)
小钢模的单方模板费用为: 50/2.5+6.8=26.8(元/m2)
则
钢木组合模板的成本指数为: 24.5/(24.5+26.8)=0.48
小钢模的成本指数为: 26.8/(24.5+26.8)=0.52
3.计算两方案的价值指数
钢木组合模板的价值指数为: 0.51/0.48=1.06
小钢模的价值指数为: 0.49/0.52=0.94
因为钢木组合模板的价值指数高于小钢模的价值指数,故应选用钢木组合模板体系。
问题3:
解:单方模板费用函数为: C=C1/Q+C2
式中:C—单方模板费用(元/m2)
C1—模板总摊销费用(万元)
C2—每平方米楼板的模板人工费(元/m2)
Q—现浇楼板工程量(万m2)
则:钢木组合模板的单方模板费用为: CZ=40/Q+8.5
小钢模的单方模板费用为: CX=50/Q+6.8
令该两模板体系的单方模板费用之比(即成本指数之比)等于其功能指数之比,有:
(40/Q+8.5)/(50/Q+6.8)=0.51/0.49
即:
51(50+6.8Q)-49(40+8.5Q)=0
所以,Q=8.46(万m2)
因此,该办公楼的现浇楼板工程量至少达到8.46万m2才应采用小钢模体系。